Post

FlashAttentionってなんだっけ

Posted Updated
By Sohei Kodama 7 min read

NeurIPS 2022 で発表された「FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness」の FlashAttention の計算方法をもう一度確認する．

FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness

背景

NLP のみならず，さまざまな分野でブレイクスルーとなった Self-Attention だが，その計算コストは大きな問題になっている． RNN と違って，Self-Attention は系列長の 2 乗に比例する計算量を持つため，長い系列に対しては非常にコストがかかる． そこで，Self-Attention の効率化に関する研究が多数行われているが，それらのほとんどは近似計算などの基づいている．

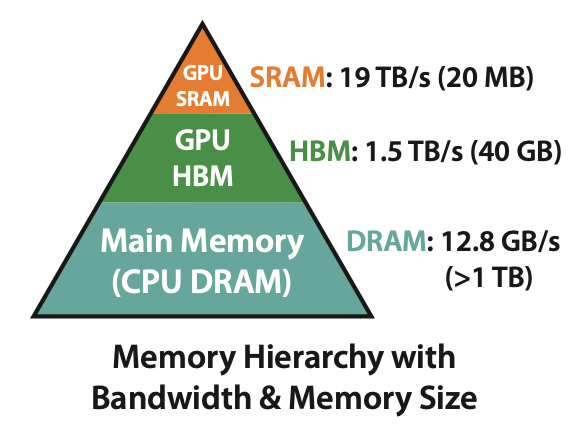
計算を行うメモリにはいくつかの階層があり，大きく CPU と GPU に分けられる． さらに，GPU メモリないで HBM と SRAM に分けられる． HBM は大容量であるが，アクセス速度が遅く，SRAM は小容量であるが，アクセス速度が速い． 機械学習の訓練は基本的に GPU で行うが，SRAM の容量が小さいため，Self-Attention の計算を全て SRAM で行うことは難しい． しかし，Self-Attention の計算を HBM に行うと，計算時間が遅くなってしまう． そこで，HBM と SRAM の両方を使いながら，計算時間を短縮する方法が求められている．

image_error

FlashAttention

FlashAttention は，Self-Attention の計算を HBM と SRAM の両方を使いながら，計算時間を短縮する手法である． 簡単に言うと，Self-Attention の計算を分割し，順番に SRAM で計算し，結果をその都度 HBM に書き込むことで，計算時間を短縮する．

準備

Self-Attention の計算を分割して，各 Q,K に対して計算した場合，Softmax の計算で問題が発生する． Softmax の計算は，$e^{QK^\top}$を計算し，行ごとに正規化を行うが，順番に計算した場合，正規化の分母が異なるため，計算結果が異なってしまう． そこで，FlashAttention では，分割された計算結果を正規化する際に，全体の正規化を考慮することで，正確な計算結果を得るようにしている．

$x\in\mathbb{R}^{B}$のベクトルがあった場合，その Softmax（scale も行う）は以下のように計算される：

\[m(x):=\max_i x_i,~~f(x):=[e^{x_1-m(x)}~\cdots~e^{x_B-m(x)}],~~l(x):=\sum_i f(x)_i,~~\text{softmax}(x):=\frac{f(x)}{l(x)}\]

二つの分割されたベクトル$x^{(1)},x^{(2)}$があった場合，それらを結合したベクトル$x$における Softmax は以下のように計算される：

\[\begin{aligned} m(x)&=m([x^{(1)}~x^{(2)}])=\max(m(x^{(1)},m^{(2)})),\\ f(x)&=[e^{m(x^{(1)})-m(x)}f(x^{(1)})~e^{m(x^{(2)})-m(x)}f(x^{(2)})],\\ l(x)&=l([x^{(1)}~x^{(2)}])=e^{m(x^{(1)})-m(x)}l(x^{(1)})+e^{m(x^{(2)})-m(x)}l(x^{(2)}),\\ \text{softmax}(x)&=\frac{f(x)}{l(x)} \end{aligned}\]

つまり，$m,l$だけ保存しておけば，二つの Softmax を一度の計算で行うことができる． FlashAttention では，この性質を利用して，Self-Attention の計算を効率化している．

計算方法

$Q,K,V\in\mathbb{R}^{N\times d}$としたとき，FlashAttention は以下のように計算される：

  1. 分割するブロックサイズの決定
    $B_c=\lceil \frac{M}{d}\rceil,B_r=\lceil \frac{M}{4d}\rceil$とする．

  2. 値の初期化
    FlashAttention の出力$O=(0)_{N\times d}\in\mathbb{R}^{N\times d}$,$l=(0)_N\in\mathbb{R}^{N}$,$m=(0)_N\in\mathbb{R}^{N}$を初期化する．ここで，$Q,K,V,O,l,m$は全て HBW に配置されている．

  3. $Q,K,V$の分割
    $Q$を$T_r=\lceil \frac{N}{B_r}\rceil$個のブロック$Q_{1},\cdots,Q_{T_r}$に分割し，$K.V$を$T_c=\lceil \frac{N}{B_c}\rceil$個のブロック$K_{1},\cdots,K_{T_c},V_{1},\cdots,V_{T_c}$に分割する．

  4. $O,l,m$の分割
    $O,l,m$を$T_r$個のブロック$O_{1},\cdots,O_{T_r},l_{1},\cdots,l_{T_r},m_{1},\cdots,m_{T_r}$に分割する．

  5. $1\leq j\leq T_c$で以下の処理を繰り返す

    1. $K_j,V_j$を HBW から SRAM に読み込む
    2. $1\leq i\leq T_r$で以下の処理を繰り返す
      1. $Q_i,O_i,l_i,m_i$を HBM から SRAM に読み込む
      2. $S_{ij}=Q_iK_j^\top\in\mathbb{R}^{B_r\times B_c}$を計算する
      3. Softmax に必要な$\tilde m_{ij},\tilde P_{ij},\tilde l_{ij}$を計算する
        $\tilde m_{ij}=\text{rowmax}(S_{ij})\in\mathbb{R}^{B_r},\tilde P_{ij}=\exp(S_{ij}-\tilde m_{ij})\in\mathbf{\mathbb{R}^{B_r\times B_c}}$，$\tilde l_{ij}=\text{rowsum}(\tilde P_{ij})\in\mathbb{R}^{B_r}$
      4. $m_i^{new},l_i^{new}$を計算する
        $m_i^{new}=\max(m_i,\tilde m_{ij}),l_i^{new}=\exp(m_i-m_i^{new})l_i+\exp(\tilde m_{ij}-m_i^{new})\tilde l_{ij}$
        この部分が準備で述べた $x^{(2)}$の方の$m,l$の計算をしている部分である．
      5. $O_i^{new}$を計算する
        $O_i^{new}=\text{diag}(l_i^{new})^{-1}(\text{diag}(l_i)\exp(m_i-m_i^{new})O_i+\exp(\tilde m_{ij}-m_i^{new})\tilde P_{ij}V_j)$
        ここが，準備の$l$を使って Softmax を計算する部分である．
      6. $O_i^{new},l_i^{new},m_i^{new}$を HBM に書き込む
        $O_i\leftarrow O_i^{new},l_i\leftarrow l_i^{new},m_i\leftarrow m_i^{new}$ と HBM に書き込む
  6. $O$を出力する

この計算方法によってメモリの使用量を$O(N)$に抑え，SRAM での Attention 計算を可能にしている

まとめ

今回は，FlashAttention の計算方法にだけ着目して説明した． backward の仕方などの細かい部分は省いたから，今度また勉強して記事にしてみたい． わかりにくかった人向けに FlashAttention の計算の流れをまとめた動画も作ったので，興味がある人は見てみてほしいです（所々間違っていたり省略したりしている部分があるが，大体の流れを把握するのにはいいと思う）．
FlashAttention の計算方法

参考文献

BLOG
Paper NLP
This post is licensed under CC BY 4.0 by the author.