Post

論文読み「Why do Nearest Neighbor Language Models Work?」

Posted Updated
By Sohei Kodama 18 min read

ICML 2023で発表された「Why do Nearest Neighbor Language Models Work?」のまとめ

Why do Nearest Neighbor Language Models Work?

概要

この論文でやったことは主に3つ

  • Retrieval-Augumented Language Models，特にkNN-LM[1]がなぜ，訓練に用いたデータをデータストアとして使用してもLMの推論をよく補正するのかを調べた
  • 逐次的に言語モデル（LM）の推論とkNN-LMの推論の差異を調べ，(1)次トークン予測における異なる表現の使用，(2)近似kNN検索，(3)kNN確率分布における温度が重要であることを特定した
  • さらにこれらの調査を活用し，検索構造を使用せず，LMに洞察を追加することによる性能の向上を実現した

導入

言語モデリングはテキストに確率を割り当てることで，様々な言語処理タスクにおいて多大な影響を及ぼしている． 一般的には，コンテキスト$c_{<t}$をモデルを表す関数$f$に入力し，次のトークン$w_t$の確率を$f(c_{<t})$に基づいて推論する．

近年では，Retriecal-Augumented LM（検索ベース言語モデル）が印象的な性能を示しており，LMによる推論だけでなく，外部のデータストアから用例を検索し，それを追加して推論を行う．Retriecal-Augumented LMの一つとして，kNN-LMがあり，構造がシンプルかつ効果的であることからよく用いられる．kNN-MT[2]はkNN-LMを機械翻訳に応用した例で，それによる効果が示されている．kNN-LMは，訓練済みLMの推論結果とkNNによって得られた推論結果を線型結合によって合成し，最終的な推論結果を計算する．

kNN-LMにおける不思議な現象として，LMを事前学習するのに用いたデータと同じデータを用いてデータストアを構築しても，性能が向上することが挙げられる．このことから，著者は「なぜkNN-LMがうまくワークするのか」と「なぜ同じデータを用いても性能が向上するのか」という疑問を抱き，この論文でそれを明らかとすることを目標とした．

kNN-LMの定式化と標準化

定式化

まずkNN-LMの詳しい説明と定式化を行う．kNN-LMは主に「データストア構築」と「推論」の2つの段階に分けられる．

データストア構築時には，訓練用データセット$\mathcal{D}$における，時点$i$以前のコンテキスト$c_{<i}$と時点$i$のトークン$w_i$のペア$(c_{<i}, w_i)\in\mathcal{D}$について，$c_{<i}$をモデルに入力した際に得られる中間表現（ベクトル）$f(c_{<i})$をキーとして，$w_i$をバリューとしてデータストア$(\mathcal{K},\mathcal{V})$に格納していく． これを定式化すると以下のようになる．

\[(\mathcal{K},\mathcal{V})=\{(f(c_{<i}), w_i)\mid(c_i,w_i)\in\mathcal{D}\}\]

一般に，モデルの中間表現$f(\cdot)$は，デコーダの最終層のFeedForward層の入力を用いる．

推論時には，LMはパラメータ$\theta$に基づいて，コンテキスト$c_{<t}$与えられたとき，次トークン$w_t$の生成確率$P_{LM}(w_t\mid c_{<t};\theta)$を計算する． 一方kNN側では，$c_{<t}$から$f(c_{<t})$を得て，それをクエリとしてデータストアに対してk近傍探索を行う．そのk個の近傍とクエリとの距離$d(\cdot,\cdot)$に用いて以下のようにkNN側の次トークン$w_t$の生成確率を計算する．

\[P_{kNN}(w_t\mid c_t)\propto\sum_{(k_i,v_i)\in\mathcal{N}} \mathbb{1}_{w_t=v_i}\exp(-d(k_i,f(c_{<t})))\]

これらの確率を重み$\lambda$で線型結合することによって最終的な次トークン$w_t$の生成確率を計算する．

\[P(w_t\mid c_{<t};\theta)=(1-\lambda)P_{LM}(w_t\mid c_{<t};\theta)+\lambda P_{kNN}(w_t\mid c_{<t}) \tag{1}\]

一般化

式(1)に注目したとき，$P_{kNN}$と$P_{LM}$の計算方法に類似点があり，kNN側ではコンテキストとデータストア内の近傍の距離をSoftmax関数で標準化して計算するが，これはクエリとなるコンテキストのベクトルから距離を計算する変換によってデータストア内の各語彙の出現確率を計算し，その上位k個を近傍として使用していると捉えられる．それに対してLM側の分布は，得られたコンテキストの埋め込みベクトルから線形変換によって各語彙の出現確率を計算する．

この解釈を利用すると，式(1)を一般化すると以下のようにかける．

\[P_{interp}=(1-\lambda)\text{softmax}(W_{sm}\cdot h_{sm}) + \lambda M\text{softmax}(\text{mask-to-k}(W_{ds}\otimes h_{ds})/\tau) \tag{2}\]

ここで，$\tau$はsoftmax関数の温度を表している． これを図にしたものがFigure 1となる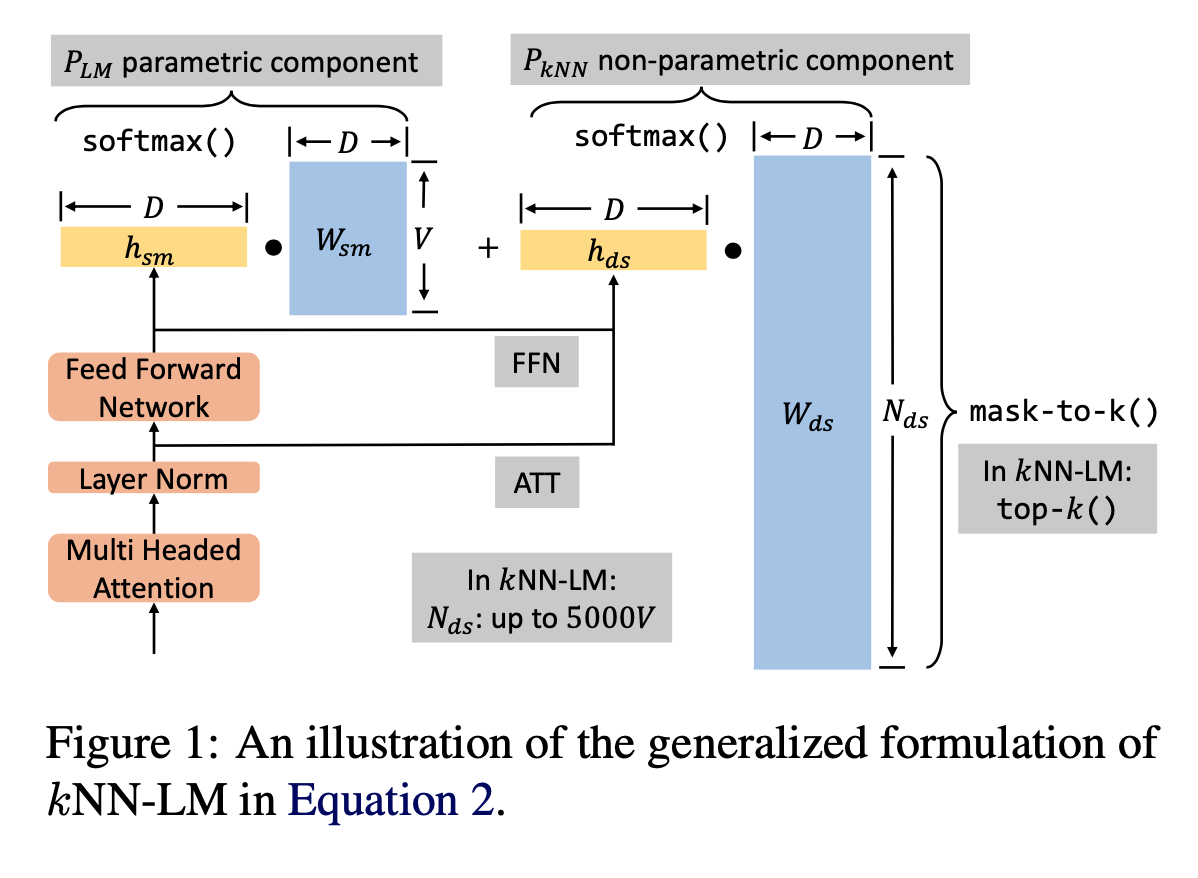． image_error

通常のkNN-LMの精度

まず，通常のkNN-LMについて実験し，クエリベクトル$h_{ds}$と変換関数$\otimes$について評価する．

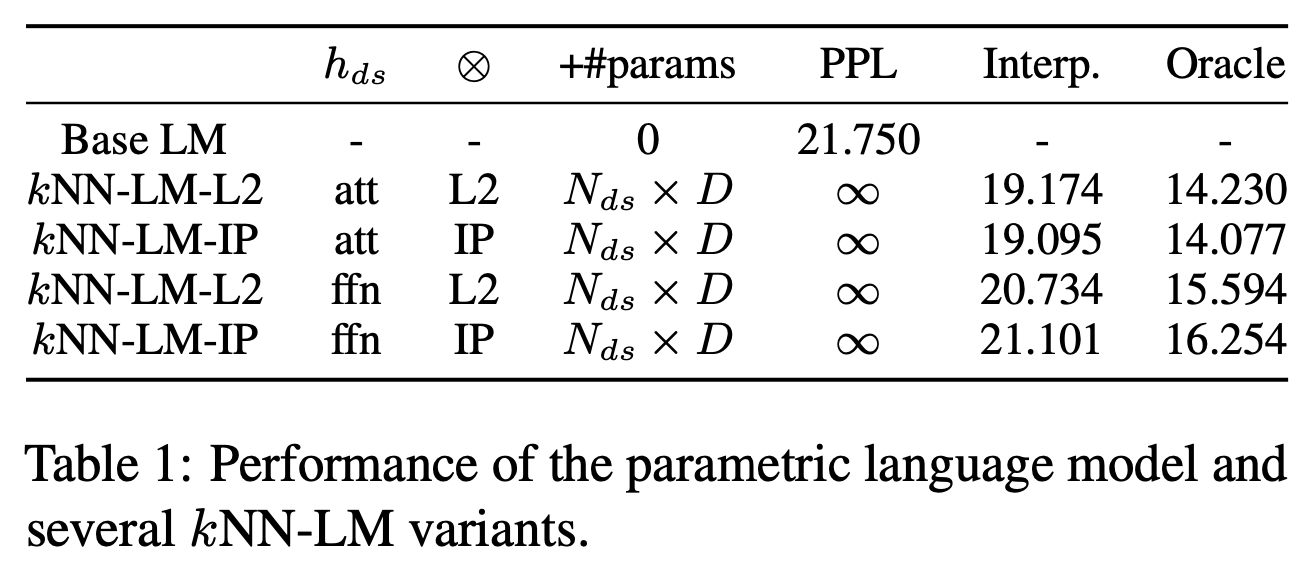
実験結果はTable 1に示されている． $h_{ds}$の列は$h_{ds}$として使用するベクトルをどこから得るかを表しており，attはSelf-Attentionの出力を表し，ffnはFeedForwardの出力を表している． $\otimes$は$\otimes$として使用する演算を表す列で，L2距離とIP（内積）で比較する． +#paramsは，LM以外に追加されたパラメータの数を表現している． PPLは$P_{kNN}$のみによって計算されたperplexityであり，Interp.は線型結合後のperplexityである． Orcleは評価用データ内の各データにおいて，重み$\lambda$を，$P_{LM}>P_{kNN}$なら$\lambda=0$とし，$P_{LM}<P_{kNN}$なら$\lambda=1$としたときである．

image_error

この結果から，クエリベクトルとしてはSelf-Attentionの出力を用いた方がよく，$\otimes$としてはL2距離でもIPでも大差がないことがわかる．

$W_{ds}$の定式化による効果

データストアの$W_{ds}$による再現

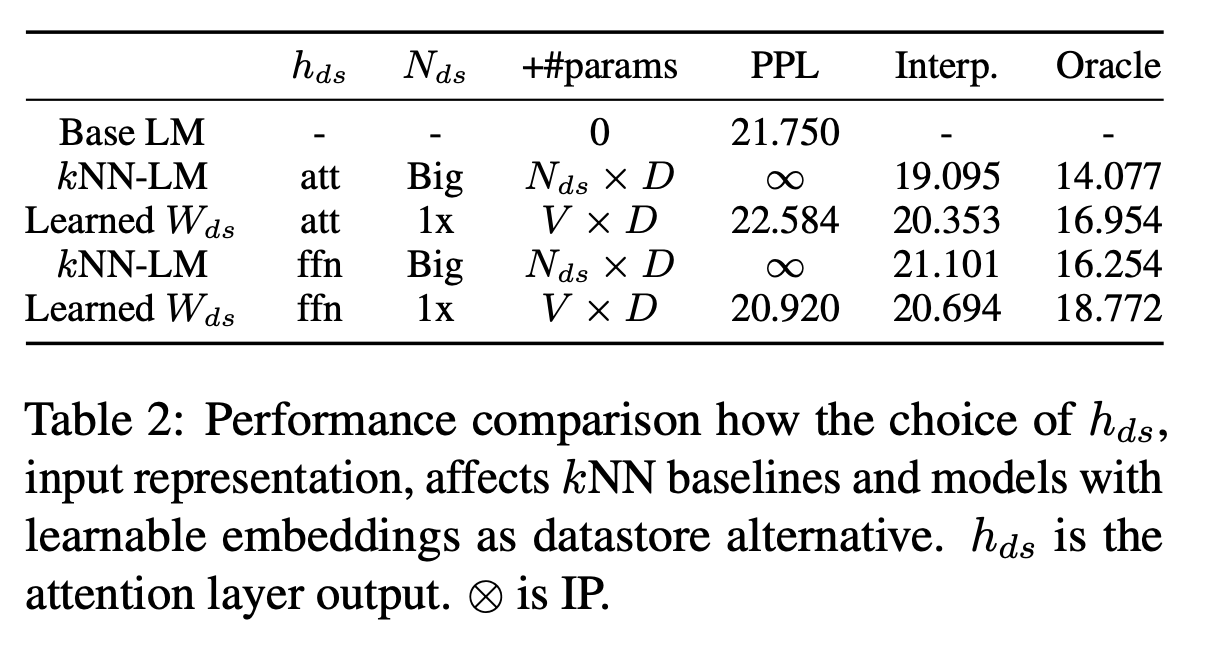
$h_{ds}$の効果をより制限された状態で検証するために，データストアを使用せず，式(2)で一般化した$W_{ds}$を訓練して実験し，その結果をTable 2に示す．

image_error

この結果から，依然としてクエリベクトルとしてはSelf-Attentionの出力を用いた方が良いことがわかる． しかし，通常のkNN-LMと訓練された$W_{ds}$を用いた場合で比較すると，パラメータの数の差に対してPerplexityの差は小さい．つまり，kNN-LMによって得られる貢献はより小さいパラメータと計算コストで再現できるということである．

データストアの規模による効果

kNN-LMの効果はデータストアに規模によるものであるという知見を検証するために，データストアの規模と$W_{ds}$のサイズと表現力による効果を検証する．

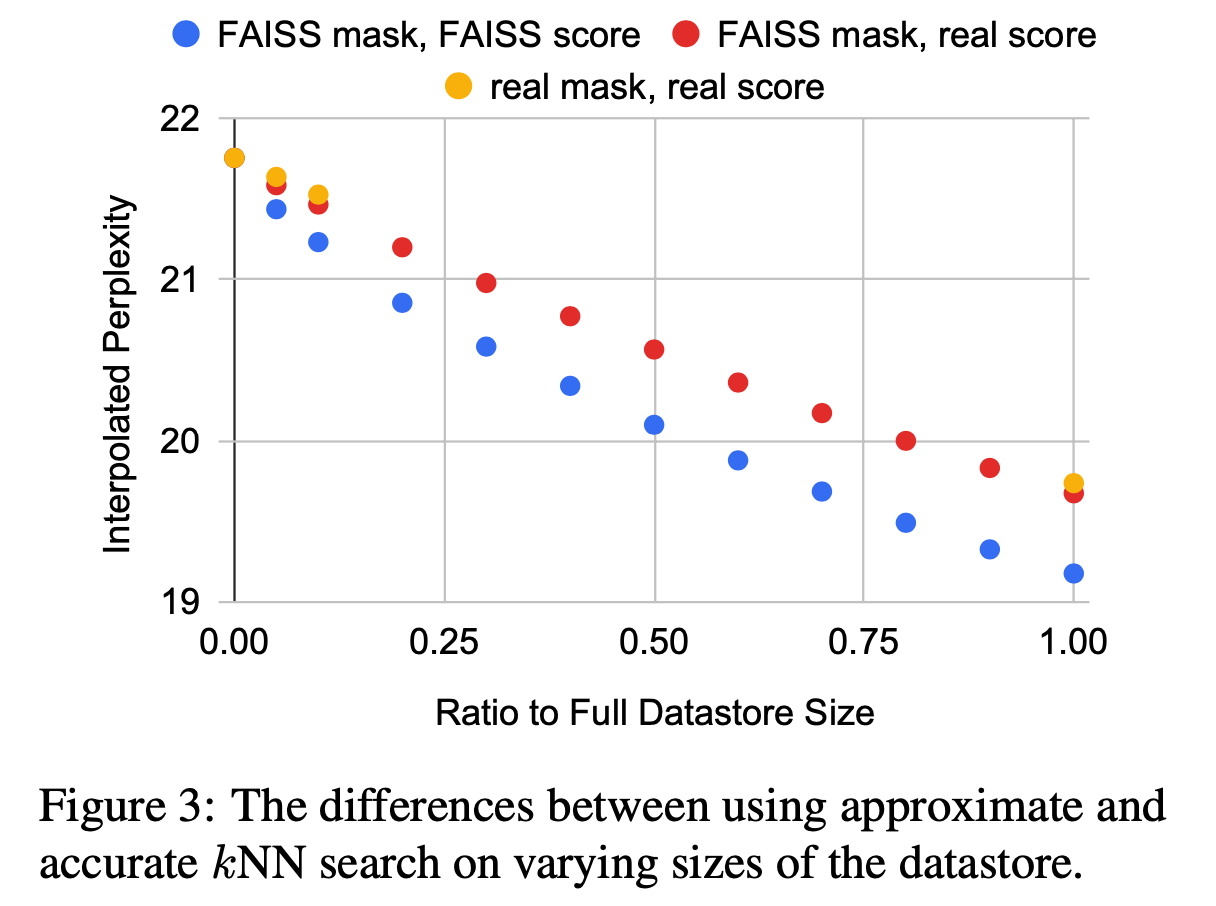
まず，データストアの規模による効果を検証するため，データストアからサブサンプルを取得し，それを用いたkNN-LMで実験を行った． その結果がFigure 3の黄点であり，サブサンプルのサイズが大きくなるとperplexityが下がることを確認した． これは，データストアのサイズがkNN-LMの性能に大きく影響することを示唆している．

image_error

この結果となった考えうる理由は，データストアのサイズによって低頻度語をカバーできるからである つまり，モデルの次元$D$では表現しきれなかった部分をデータストアのサイズ$N_{ds}$によって表現できるようになっているということである． この仮説を検証するため，$W_{ds}$のサイズを変化させ，比較実験を行った．

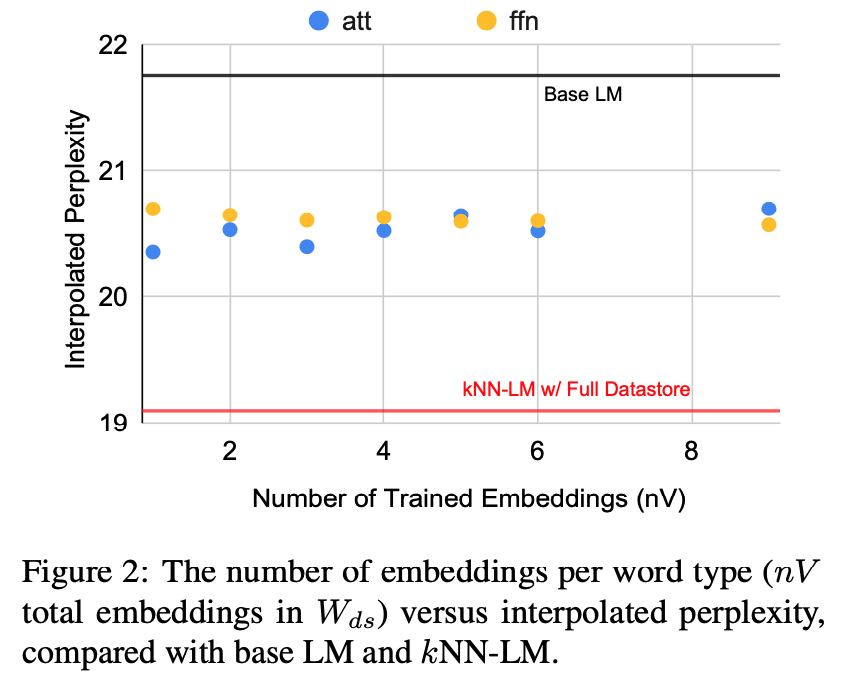
$W_{ds}$のサイズを$N_{ds}\times D$からtokenizerの語彙数$V$によって，$nV\times D$と変化させる． その結果がFigure 2であり，$n$を変化させても大きく結果が変化しないことがわかったが，元のデータストアのサイズは約5000Vであるため，サイズによる影響は多少あると考えられる．

image_error

この結果から，データストアのサイズによる低頻度語のカバーにより，性能が向上されているのかと考えられる．

（これについて調べた論文がNLP2024にて発表されており，この仮説は否定されている）

近似近傍探索とSoftmax温度による効果

近似近傍探索による効果

通常のkNN-LMでは，データストアに対して網羅的な近傍探索を行わず，FAISSによる近似近傍探索を行っている． FAISSは主に二つの近似をおこなっている．

  1. 近似mask（近傍）: 全探索を避け，いくつかのクラスタに分けて探索を行う
  2. 近似score: 距離計算における近似

この近似を操作しておこなった実験の結果がTable 3である． 近似をおこなっていないkNN-LM（real mask, real score）よりも，mask・scoreともに近似をおこなっている方が性能が良い．

image_error

また，データストアのサイズを変化させた実験において，FAISSによる効果を確認したところ，同様に近似を行なっていない場合よるも近似を行なっている場合の方が精度が高いことがわかった．

image_error

著者はこの結果は，近似によって過学習が抑制されているからだと考えている．

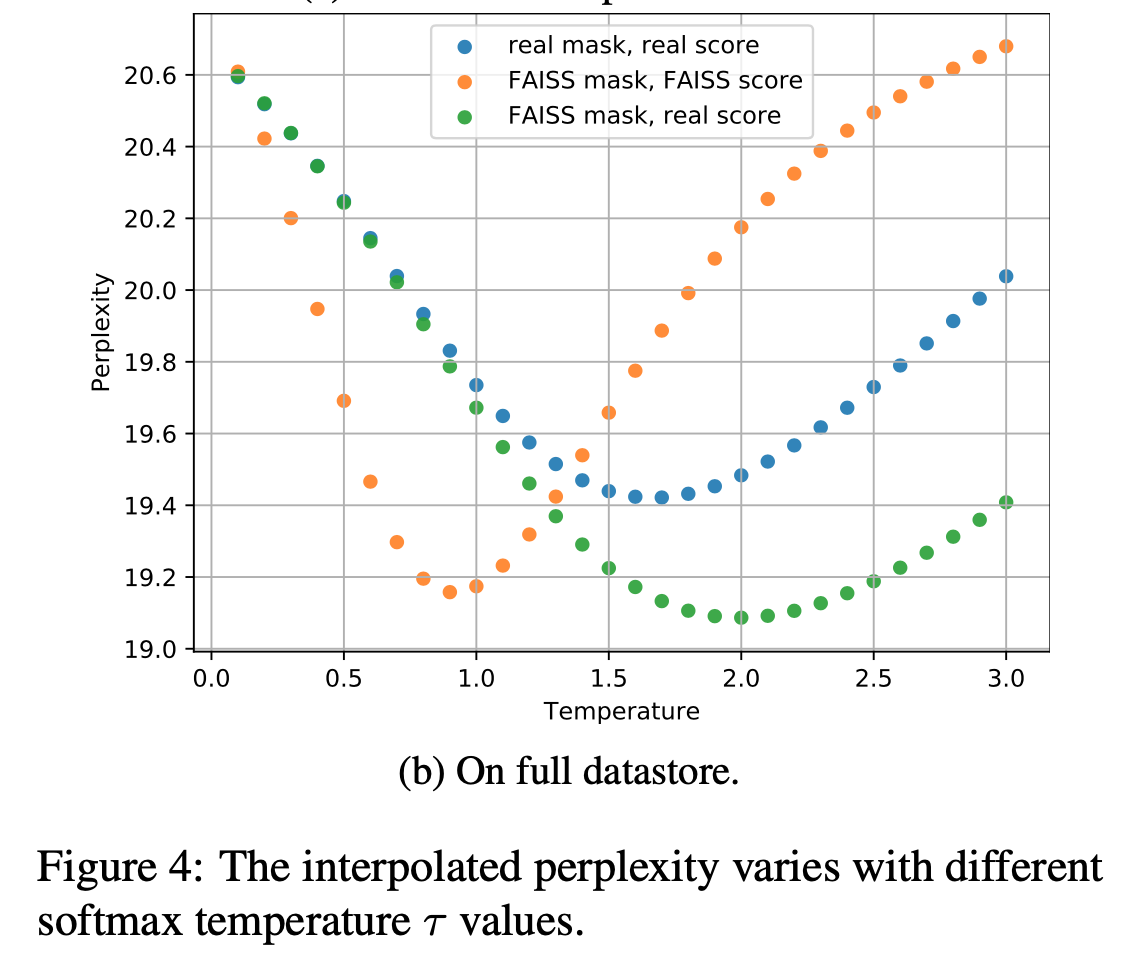
Softmax温度による効果

近傍探索数$k$は語彙数$V$と比べると非常に小さいため，$P_{kNN}$におけるピークは$P_{LM}$よりも高くなる傾向がある． そのピークを調整するのが，softmax関数の温度$\tau$である． $\tau$を0~3まで0.1刻みで変化させた時の結果がFigure 4である．

image_error

$\tau=1$が常に最適であるわけではなく，Softmax温度を調整することが重要であることがわかった．

結論

この論文では，同じトレーニングデータを用いていても，なぜkNN-LMがパープレキシティを改善するかを調査した． さまざまな仮説を提案し，検証したことで，kNN-LMの成功の鍵は以下の3つであることがわかった：

  1. 異なる入力表現（フィードフォワードレイヤーの出力とアテンションレイヤーの出力）でアンサンブルされていること
  2. 近似最近傍検索を使用することで、kNN-LMが正確な最近傍検索よりも汎化能力が高まり、正則化効果を及ぼしている
  3. kNN分布のsoftmax温度を調整することは、基本となるLMの出力分布を調整する上で重要となる

感想

いくつかの実験によってなぜうまくいくかはわかったが，まだ完全にkNN-LMの効果を調査しきれていない気がする． というのも，この論文の仮説であった，kNN-LMは低頻度語の生成を助けるという仮説は最近否定されたことから，いくつか再検証する必要があると思う．

参考文献

[1] https://arxiv.org/abs/1911.00172
[2] https://arxiv.org/abs/2010.00710

BLOG
Paper NLP
This post is licensed under CC BY 4.0 by the author.